文章编号: 0258-8013(2021)17-5827-15 中图分类号: TM72 文献标识码: A
2. 国网厦门供电公司,福建省 厦门市 361004
2. State Grid Xiamen Power Supply Company, Xiamen 361004, Fujian Province, China
直流配电网作为智能电网中的重要组成部分,由于其不考虑无功、频率和功角问题,对经各并网单元进行功率传输的精确控制是系统稳定运行的首要问题,而直流电压间接地反映有功功率的平衡,对其控制方法的研究具有重要意义。控制方式的制定必须考虑系统电压等级和拓扑结构等因素,例如并网状态、电压控制单元类型、负荷类型、控制器带宽等。目前较为成熟的电压控制方式,如定直流电压控制、定有功功率控制、主从控制、裕度控制、下垂控制等,在针对不同应用场景应用时均表现出一定程度的局限性[1-7]。
对于直流配网母线电压控制方式的研究,首先应明确承担此任务的控制单元,即通过自身电力电子开断元件以调节交流大电网或分布式能源与直流系统交换功率,最终达到母线电压控制的效果。在直流电网联网情况下,目前主要还是依靠交直流换流站完成此任务,但也有学者提出在多节点直流配网中储能等分布式能源可参与电压控制[4-5, 8-9]。文献[10]通过量化交直流端口虚拟惯性和配网-微网端口电压变化机理,提出一种考虑分布式储能参与的电压柔性控制策略。当交直流换流站承担电压稳定任务时,系统内必须至少有一个换流站保证母线电压水平,因此可在全部换流站中选择其中一个(主换流站)工作于定电压控制模式,其余换流站(从换流站)工作于定功率控制模式,当主换流站达到功率限额时,选取其它换流站作为主换流站,这就是主从控制和裕度控制的基本思路[11]。为解决系统中控制方式切换繁琐的问题,文献[12]提出了一种P-U-I控制器,简化了工作模式切换问题。
直流下垂控制是在交流系统下垂控制的基础上提出的,是目前应用较多的站间协调控制方式,过程中无需上层控制器参与,也无需利用通信系统,具有较好的模块性和扩展性。但其缺点也十分明显,首先为适应不同容量换流站和不同负荷水平的运行工况,一个准确的下垂系数对系统稳定运行起着十分重要的作用,选取不准确时会严重影响母线电压的稳定控制; 其次,由于传统下垂控制相较于主从控制模式对线路阻抗敏感程度更高,当计及传输线路阻抗时,较小的下垂系数能够保证较小的直流母线电压偏差,而下垂系数偏小会在一定程度上影响系统响应速度和功率分配精度[13],下垂控制运行结果也会存在稳态误差等问题[6]。
上述提到的考虑线路阻抗时传统下垂控制存在不可避免的缺陷,文献[13]针对多换流器并联为公共负荷供电的情况,首次提出了全局下垂控制器(universal droop controller,UDC),实现在准确分配功率的同时消除线路阻抗的影响,兼顾了跟踪稳定性和系统响应速度的不足。但需注意的是,该控制器是在换流器输出阻抗为阻性时提出的,因此为消除其在含各类型换流器输出阻抗和馈线系统中应用时的限制,文献[14]对换流器输出阻抗角度在范围内的情况进行分析,结果表明,UDC控制器对于任何阻抗类型均适用,都能同时实现准确的功率分配和电压跟踪。目前,UDC在直流配电网中的应用较少,文献[15]将UDC用于直流配电网DC-DC变流器参与母线电压控制,弥补了传统下垂控制的不足。此外,基于传统PI控制进行设计时一般默认系统中各类参数为恒定值,然而直流网络中各类源荷的连接与断开,直流馈线的参数变化均会影响换流器等效电容和电感的变化,进而影响系统正常运行。鲁棒控制器可同时满足系统的鲁棒稳定性和跟踪性,消除系统参数摄动和外部输入干扰的影响。文献[16]在不考虑系统非线性摄动的情况下,利用前馈控制方法推导出一种2自由度定电压鲁棒控制器。文献[17]利用类似方法,提出一种基于传统下垂的直流母线电压鲁棒控制器,但其中没有考虑计及直流线路阻抗时各换流站等比例承担功率/电流的问题。
本文针对传统下垂控制的不足,提出一种应用于直流配网电压源换流器的全局下垂控制器,以减小母线电压偏差,保证各电压源型换流器(voltage source converter,VSC)直流侧输出电流成比例。然后,在考虑VSC交直流侧内部损耗和瞬时功率的基础上,从非结构化不确定性和参数化不确定性两方面推导分析直流侧电压的小信号控制模型,从而基于μ-综合方法进行2自由度鲁棒控制器设计。与现有文献的设计方法不同,本文对控制结构进行非结构化不确定性和参数化不确定性建模分析,对应于简化电流控制器和较为直观的系统参数,分别消除非线性扰动和系统参数变化对输出电压的影响。最后,通过稳定性分析和仿真结果验证该控制器的有效性。
1 考虑交直流侧瞬时功率的全局下垂控制VSC小信号建模 1.1 下垂控制特性分析以直流电网换流器U-I下垂控制为例,其直流侧出口参考电压为
| $U_{\text{dc}i}^ * = {U_{\text{n}i}} - {d_i}{I_i}$ | (1) |
式中:Uni为空载情况下的源换流器电压设定值;
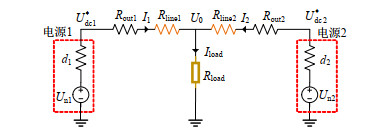
图 1为由两个源换流器、线路阻抗和负荷组成的等效稳态直流配电网电路[8],其中:Un1、Un2分别空载情况下源换流器1和2的电压设定值; Rout1、Rout2为换流器输出阻抗(除虚拟阻抗外); Rline1、Rline2为线路阻抗; Iload和U0分别为负载电流和电压。
|
图 1 简化直流配网电路 Fig. 1 Simplified DC distribution network circuit |
假设Un2=Un1=Un,由图 1可知,两换流器出口电压参考值偏差为
| $\varDelta U_{\text{dc}}^\text{*} = \frac{{{U_\text{n}} - {U_0}}}{{({R_{\text{out}1}} + {R_{\text{line1}}}){\rm{/}}{d_1} + 1}} - \frac{{{U_{\rm{n}}} - {U_0}}}{{({R_{\text{out}2}} + {R_{\text{line}2}}){\rm{/}}{d_2} + 1}}$ | (2) |
为满足换流器按各自额定容量分配电流,式(2)应恒等于0,其充分不必要条件为
| $\frac{{{d_1}}}{{{R_{\text{out1}}} + {R_{\text{line}1}}}} = \frac{{{d_2}}}{{{R_{\text{out}2}} + {R_{\text{line2}}}}}$ | (3) |
式(3)表明,换流器下垂系数应与换流器输出阻抗和线路阻抗之和成正比,这个条件对于包含数值计算误差、外界干扰和参数摄动等因素的系统来说是较为严苛的。
1.1.1 电流分配偏差假设Un=Un1=Un2,由式(1)可知,电流分配偏差ΔIi可由换流出口电压参考值偏差
| $\varDelta {I_i} = - \frac{{\varDelta U_{\text{dc}i}^ * }}{{{d_i}}}$ | (4) |
两换流器对负荷供电时的直流电流分配偏差为
| $\begin{array}{l} {e_{\rm{I}}}\% = \frac{{\varDelta {I_1}}}{{I_1^ * }} - \frac{{\varDelta {I_2}}}{{I_2^ * }} = \frac{{\varDelta U_{\text{dc}2}^ * }}{{{d_2}I_2^ * }} - \frac{{\varDelta U_{\text{dc}1}^ * }}{{{d_1}I_1^ * }} = \\ \;\;\;\;\;\;\;\;\;\frac{{\varDelta U_{\text{dc}}^\text{*}}}{{{d_i}I_i^ * }} = \frac{{{U_\text{n}}}}{{{d_i}I_i^ * }}\frac{{\varDelta U_{\text{dc}}^ * }}{{{U_\text{n}}}}\begin{array}{*{20}{c}} {}&{, i = 1, 2} \end{array} \\ \end{array} $ | (5) |
假设di=d1=d2≠0且Un=Un1=Un2,由式(2)可知:
| ${U_0} = {U_\text{n}} - \frac{1}{{\frac{1}{{{d_2} + {R_{\text{out}2}} + {R_{\text{line}2}}}} + \frac{1}{{{d_1} + {R_{\text{out}1}} + {R_{\text{line1}}}}}}}{I_\text{n}}$ | (6) |
假设
| $\begin{array}{l} {U_0} = {U_\text{n}} + ({d_2} + {R_{\text{out}2}} + {R_{\text{line}2}})I_i^ * - \\ \;\;\;\;\;\;\;\;({d_2} + {R_{\text{out}2}} + {R_{\text{line2}}}){I_\text{n}} \\ \end{array} $ | (7) |
假设Un=Un1=Un2,系统损耗为
| ${P_{\text{loss}}} = \frac{1}{{\frac{1}{{{d_2} + {R_{\text{out}2}} + {R_{\text{line}2}}}} + \frac{1}{{{d_1} + {R_{\text{out}1}} + {R_{\text{line}1}}}}}}I_\text{n}^\text{2}$ | (8) |
假设
| $\begin{array}{l} {P_{\text{loss}}} = ({d_2} + {R_{\text{out2}}} + {R_{\text{line2}}})I_\text{n}^2 - 2I_1^ * ({d_2} + {R_{\text{out}2}} + {R_{\text{line}2}}) \\ \;\;\;\;\;{I_\text{n}} + ({d_1} + {R_{\text{out}1}} + {R_{\text{line}1}} + {d_2} + {R_{\text{out}2}} + {R_{\text{line}2}}){(I_1^ * )^2} \\ \end{array} $ | (9) |
前面已经对系统满足Un=Un1=Un2时的情况进行了分析,对于由系统本身设置或传感误差造成的源参考电压信号不相等(Un1≠Un2)的情况,电流将变为
| ${I_1} = \frac{{{d_2} + {R_{\text{out2}}} + {R_{\text{line}2}}}}{{{d_1} + {R_{\text{out}1}} + {R_{\text{line1}}}}}{I_2} + \frac{{{U_{\text{n}1}} - {U_{\text{n}2}}}}{{{d_1} + {R_{\text{out}1}} + {R_{\text{line1}}}}}$ | (10) |
第二项为新增项,即由参考电压不相等造成的电流分配误差,且不随负荷水平而变化,只与系统设置、传感精度和下垂系数有关。
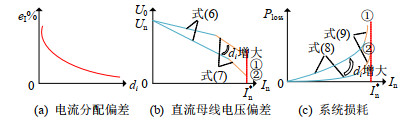
图 2即为下垂控制工作特性,可以看出:电流偏差与下垂系数大小成反比; 而母线电压偏差与下垂系数成正比,并且随着负荷水平增加母线电压偏差也逐渐增大; 除此之外,系统损耗与下垂斜率成正比,当负荷水平增加时,损耗也变大。
|
图 2 下垂控制工作特性 Fig. 2 Droop control characteristics |
总的来说,采用下垂控制时,为了使多个并联换流器按各自额定容量承担系统电流/功率,换流器应该有相同的阻抗标幺值并且各个微源设置的额定电压值也应该相同,否则从保证电流分配精度和减小恒功率负载(constant power load,CPL)影响的角度来说,需要设置较大的下垂系数; 而从直流母线电压精准控制和降低系统功率损耗的角度来说,需要较小的下垂系数,因此传统下垂控制不能兼顾以上性能要求[7]。
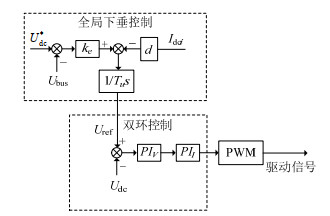
1.2 全局下垂控制为解决传统下垂控制应用时的不足,本文提出全局下垂VSC控制器,如图 3所示,其中:
|
图 3 电压源换流器全局下垂原理 Fig. 3 Universal droop controller of voltage source converter |
并网系统稳态运行时,积分器输入为0,即:
| ${d_i}{I_{\text{dc}i}} = {K_e}(U_{\text{dc}}^\text{*} - {U_{\text{bus}}})\begin{array}{*{20}{c}} {}&{i = 1, 2, \cdots , n} \end{array}$ | (11) |
式中n为并联于直流母线换流器个数(下同)。此时只要选择相同的Ke,右半部分对并联于直流母线的所有换流器来说都相等,即有:
| ${d_1}{I_{\text{dc1}}} = {d_2}{I_{\text{dc}2}} = \cdots \cdots = {d_n}{I_{\text{dc}n}}$ | (12) |
即:
| $\frac{{{d_1}}}{{{d_2}}} = \frac{{{I_{\text{dc}2}}}}{{{I_{\text{dc}1}}}} = \frac{{I_2^ * }}{{I_1^ * }}$ | (13) |
式中
作为交直流系统中间联接单元,VSC交流侧储能单元会带来其内部瞬时潮流变化,直流母线电压的小信号动态响应可能会由逆变运行状态的最小相位系统变为整流运行状态的非最小相位系统,从而影响直流电压控制的稳定性。同样对于直流侧储能单元来说,当在直流电压输入输出方程中加入其瞬时功率时,同样会因为换流器工作状态不同而改变传递函数的零点分布,从而导致母线电压受到影响,目前国内外对此研究较少。文献[18]虽然对此有过研究,但精细化程度不高,仍然存在以下2点问题:
1) 考虑了换流器和开关器件的功率损耗Ploss,但在定义直流侧直流电流时没有计及对应电流iloss;
2) 考虑直流侧电容瞬时功率时,没有计及新加入的直流侧电感带来的压降,而把换流器直流侧电压Udc当作电容电压UCeq。
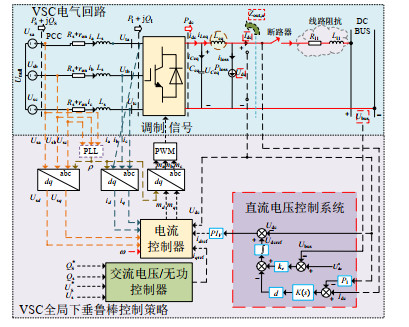
1.3.1 并网VSC拓扑结构本文采用图 4所示的矢量控制两电平VSC换流器,Ls为联结变压器和电抗器的等效电感和变压器漏感之和(由于直流电压控制环的带宽一般小于基础频率,在此范围内VSC交流侧滤波器主要表现为L型[17]),Rs+ron为联结变压器和电抗器等效电阻,其中ron为VSC损耗等效电阻,Ploss为开关的反向恢复和跟踪电流过程造成的功率损耗,iloss为对应电流,Ceq为直流侧等效电容,UCeq为电容电压,iCeq为直流侧电容电流,Leq为直流侧等效电感,iLeq为电感电流,Rl和Ll分别为换流器直流侧线路电阻和电感,Usa、Usb、Usc为交流系统三相电压,Uta、Utb、Utc为换流器交流侧三相电压。Ps、Qs分别为系统交流侧公共连接点的有功和无功功率,Pt、Qt分别为换流器交流侧的有功功率和无功功率,Udc、Idc分别为换流器直流侧连接直流线路出口处的直流电压和电流,Pdc为换流器直流侧有功功率,idc为换流器直流侧电流,需注意Pdc≠IdcUdc。
|
图 4 VSC控制结构 Fig. 4 VSC control framework |
本文中的换流器采用以电网电压为参考方向的标准矢量控制方法,Usq=0,因此交流系统在图 4中PCC处传输的功率为
| ${P_{\text{PCC}}} = 1.5{U_{\text{sd}}}{I_d} + 1.5{U_{\text{sq}}}{I_q} = 1.5{U_{\text{sd}}}{I_d}$ | (14) |
考虑直流侧滤波器瞬时功率时,换流器交直流侧功率平衡方程为
| $\begin{array}{l} 1.5{U_{\text{sd}}}{I_d} - D{W_L} - {P_R} = D(0.5{C_{\text{eq}}}U_{C\text{eq}}^2) + \\ \;\;\;\;D(0.5{L_{\text{eq}}}i_{L\text{eq}}^2) + {P_{\text{loss}}} + {I_{\text{dc}}}{U_{\text{dc}}} \\ \end{array} $ | (15) |
式中:等式左侧为换流器交流侧功率Pt; 等式右侧为换流器直流侧功率Pdc,D为对时间的微分因子,Dx=d(x)/dt; WL为交流侧等效电感的能量; PR为交流侧等效电阻R(Rs和ron之和)的功率; |I|为dq坐标系下交流侧电流的模。
对于换流器交流侧而言,功率平衡方程为
| $1.5{U_{\text{sd}}}{I_d} - D{W_\text{t}} - {P_R} - {P_\text{t}} = 0$ | (16) |
继而有:
| ${P_R} = \operatorname{Re} \{ 1.5R\vec I(t){\vec I^ * }(t)\} = 1.5R{\rm{|}}I{{\rm{|}}^2} = 1.5R(I_d^2 + I_q^2)$ | (17) |
式中:|I|为dq坐标系下交流侧电流的模;
对于交流侧三相电感,其储存能量为
| ${W_L} = 0.75{L_\text{s}}{I^2} = 0.75{L_\text{s}}(I_d^2 + I_q^2)$ | (18) |
将式(17)和(18)代入式(16)可得到函数F:
| $\begin{array}{l} 1.5{U_{\text{sd}}}{I_d} - 1.5{L_\text{s}}{I_d}D{I_d} - 1.5{L_\text{s}}{I_q}D{I_q} - 1.5R(I_d^2 + I_q^2) - \\ \;\;\;\;{P_\text{t}} = 0 = F({U_{\text{sd}}}, {I_d}, D{I_d}, {I_q}, D{I_q}, {P_\text{t}}) \\ \end{array} $ | (19) |
由于式(19)为非线性方程,可利用泰勒级数对动态方程F在稳态运行点(equilibrium point,E.P.)进行展开:
| $\begin{array}{l} {\rm{F}}({U_{\text{sd}}}, {I_d}, D{I_d}, {I_q}, D{I_q}, {P_t}) = {\left. {\rm{F}} \right|_{\text{(E}\text{.P}\text{.)}}} + \frac{{\partial F}}{{\partial {U_{\text{sd}}}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {U_{\text{sd}}} + \\ \;\;\;\frac{{\partial F}}{{\partial {I_d}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {I_d} + + \frac{{\partial F}}{{\partial (D{I_d})}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta (D{I_d}) + \frac{{\partial F}}{{\partial {I_q}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {I_q} + \\ \;\;\frac{{\partial F}}{{\partial (D{I_q})}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta (D{I_q}) + + \frac{{\partial F}}{{\partial {P_t}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {P_t} + \text{(H}\text{.O}\text{.T)} = 0 \\ \end{array} $ | (20) |
式中:Δ为小信号量; (H.O.T)为展开时产生的高阶项,在此忽略不计。系统稳态运行点可表示为
| $\begin{array}{l} \text{(E}\text{.P}\text{.)} = ({U_{\text{sd - 0}}}, {I_{d\text{ - }0}}, D{I_{d\text{ - }0}}, {I_{q\text{ - }0}}, D{I_{q\text{ - }0}}, {P_{\text{t - 0}}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;({U_{\text{sd0}}}, {I_{d0}}, 0, {I_{q0}}, 0, {P_{\text{t0}}}) \\ \end{array} $ | (21) |
将其代入式(20)可得:
| $\begin{array}{l} \varDelta {P_\text{t}} = 1.5{I_{d0}}\varDelta {U_{\text{sd}}} + 1.5{U_{\text{sd0}}}\varDelta {I_d} - 1.5{L_\text{s}}{I_{d0}}\varDelta (D{I_d}) - \\ \;\;\;\;\;\;\;\;\;1.5{L_\text{s}}{I_{q0}}\varDelta (D{I_q}) - 3R{I_{d0}}\varDelta {I_d} - 3R{I_{q0}}\varDelta {I_q} \\ \end{array} $ | (22) |
对上式进行拉氏变换可得(省略了拉普拉斯算子s,下同):
| $\begin{array}{l} \varDelta {P_\text{t}} = 1.5{I_{d0}}\varDelta {U_{\text{sd}}} + ( - 1.5{L_s}{I_{d0}}{\rm{s}} + 1.5{U_{sd0}} - 3R{I_{d0}}) \\ \;\;\;\;\;\;\;\;\varDelta {I_d} - (1.5{L_s}{I_{q0}}s + 3R{I_{q0}})\varDelta {I_q} \\ \end{array} $ | (23) |
式(23)即为换流器交流侧有功功率Pt的小信号动态方程。
1.3.3 VSC直流侧动态方程小信号建模由式(15)可知,换流器直流侧功率为
| ${P_{\text{dc}}} = D(0.5{C_{\text{eq}}}U_{C\text{eq}}^2) + D(0.5{L_{\text{eq}}}i_{L\text{eq}}^2) + {P_{\text{loss}}} + {I_{\text{dc}}}{U_{\text{dc}}}$ | (24) |
根据图 4,有直流侧相关电压、电流关系式:
| $\left\{ {\begin{array}{*{20}{l}} {{i_{L\text{eq}}} = {I_{\text{dc}}} + {P_{\text{loss}}}{\rm{/}}{U_{\text{dc}}}} \\ {{U_{C\text{eq}}} = {U_{\text{dc}}} + {L_{\text{eq}}}D{i_{L\text{eq}}}} \end{array}} \right.$ | (25) |
考虑交直流功率相等即Pt=Pdc时,将式(25)代入式(24)可得:
| $\begin{array}{l} D(0.5{C_{\text{eq}}}{({U_{\text{dc}}} + {L_{\text{eq}}}D{i_{L\text{eq}}})^2}) + D(0.5{L_{\text{eq}}}i_{L\text{eq}}^2) + \\ \;\;\;{P_{\text{loss}}} + {I_{\text{dc}}}{U_{\text{dc}}} - {P_\text{t}} = 0 \\ \end{array} $ | (26) |
将式(26)展开为
| $\begin{array}{l} {C_{\text{eq}}}{U_{\text{dc}}}D{U_{\text{dc}}} + 0.5{C_{\text{eq}}}L_{\text{eq}}^\text{2}(2D{I_{\text{dc}}}{D^2}{I_{\text{dc}}} + {P_1} + {P_2}) + \\ \;\;\;\;{C_{\text{eq}}}{L_{\text{eq}}}(D{I_{\text{dc}}}D{U_{\text{dc}}} + ({D^2}{I_{\text{dc}}}){U_{\text{dc}}}) + {P_3} + {P_4} + \\ \;\;\;\;{P_{\text{loss}}} + {I_{\text{dc}}}{U_{\text{dc}}} - {P_\text{t}} = 0 = G({U_{\text{dc}}}, D{U_{\text{dc}}}, {D^2}{U_{\text{dc}}}, \\ \;\;\;\;\;{I_{\text{dc}}}, D{I_{\text{dc}}}, {D^2}{I_{\text{dc}}}, {P_{\text{loss}}}, D{P_{\text{loss}}}, {D^2}{P_{\text{loss}}}, {P_\text{t}}) \\ \end{array} $ | (27) |
其中:
| $\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {P_1} = \frac{{2D{P_{\text{loss}}}{D^2}{P_{\text{loss}}}U_{\text{dc}}^\text{2} - {{(D{P_{\text{loss}}})}^2} \cdot 2{U_{\text{dc}}}D{U_{\text{dc}}}}}{{U_{\text{dc}}^4}} + \\ \;\;\;\;\;\;\frac{{(2{P_{\text{loss}}}D{P_{\text{loss}}}{{(D{U_{\text{dc}}})}^2} + P_{\text{loss}}^22D{U_{\text{dc}}}{D^2}{U_{\text{dc}}})U_{\text{dc}}^\text{4} - P_{\text{loss}}^2{{(D{U_{\text{dc}}})}^2} \cdot 4{U_{\text{dc}}}D{U_{\text{dc}}}}}{{U_{\text{dc}}^\text{8}}} - \\ \;\;\;\;\;\;\frac{{2({{(D{P_{\text{loss}}})}^2}D{U_{\text{dc}}} + {P_{\text{loss}}}{D^2}{P_{\text{loss}}}D{U_{\text{dc}}} + {P_{\text{loss}}}D{P_{\text{loss}}}{D^2}{U_{\text{dc}}})U_{\text{dc}}^\text{3} - 6{P_{\text{loss}}}D{P_{\text{loss}}}{{(D{U_{\text{dc}}})}^2}U_{\text{dc}}^{}}}{{V_{\text{dc}}^\text{6}}} \\ \end{array} \\ \begin{array}{l} {P_2} = \frac{{2({D^2}{I_{\text{dc}}}D{P_{\text{loss}}} + D{I_{\text{dc}}}{D^2}{P_{\text{loss}}})U_{\text{dc}}^{} - 2DI_{\text{dc}}^{}D{P_{\text{loss}}}D{U_{\text{dc}}}}}{{U_{\text{dc}}^2}} - \\ \;\;\;\;\;\;\;\frac{{2({D^2}{I_{\text{dc}}}{P_{\text{loss}}}D{U_{\text{dc}}} + D{I_{\text{dc}}}D{P_{\text{loss}}}D{U_{\text{dc}}} + D{I_{\text{dc}}}{P_{\text{loss}}}{D^2}{U_{\text{dc}}}) - 4D{I_{\text{dc}}}{P_{\text{loss}}}{U_{\text{dc}}}{{(D{U_{\text{dc}}})}^2}}}{{U_{\text{dc}}^\text{4}}} \\ \end{array} \\ {{P_3} = {C_{\text{eq}}}{L_{\text{eq}}}{D^2}{P_{\text{loss}}} - {C_{\text{eq}}}{L_{\text{eq}}}\frac{{(D{P_{\text{loss}}}D{U_{\text{dc}}} + {P_{\text{loss}}}{D^2}{U_{\text{dc}}}){U_{\text{dc}}} - {P_{\text{loss}}}{{(D{U_{\text{dc}}})}^2}}}{{U_{\text{dc}}^2}}} \\ {{P_4} = {L_{\text{eq}}}({I_{\text{dc}}}D{I_{\text{dc}}} + \frac{{{P_{\text{loss}}}D{P_{\text{loss}}}U_{\text{dc}}^2 - P_{\text{loss}}^\text{2}{U_{\text{dc}}}D{U_{\text{dc}}}}}{{U_{\text{dc}}^\text{4}}} + \frac{{(D{I_{\text{dc}}}{P_{\text{loss}}} + {I_{\text{dc}}}D{P_{\text{loss}}}){U_{\text{dc}}} - {I_{\text{dc}}}{P_{\text{loss}}}D{U_{\text{dc}}}}}{{U_{\text{dc}}^\text{2}}})} \end{array}} \right.$ | (28) |
利用泰勒级数对式(27)中的动态方程G在稳态运行点展开:
| $\begin{array}{l} {\rm{G}}({U_{\text{dc}}}, D{U_{\text{dc}}}, {D^2}{U_{\text{dc}}}, {I_{\text{dc}}}, D{I_{\text{dc}}}, {D^2}{I_{\text{dc}}}, {P_{\text{loss}}}, D{P_{\text{loss}}}, \\ \;\;\;{\left. {{D^2}{P_{\text{loss}}}, {P_\text{t}}) = {\rm{G}}} \right|_{\text{(E}\text{.P}\text{.)}}} + \frac{{\partial G}}{{\partial {U_{\text{dc}}}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {U_{\text{dc}}} + \frac{{\partial G}}{{\partial ({\rm{D}}{U_{\text{dc}}})}}{|_{\text{(E}\text{.P}\text{.)}}} \\ \;\;\;\varDelta ({\rm{D}}{U_{\text{dc}}}) + \frac{{\partial G}}{{\partial ({{\rm{D}}^2}{U_{\text{dc}}})}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta ({{\rm{D}}^2}{U_{\text{dc}}}) + \frac{{\partial G}}{{\partial {I_{\text{dc}}}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {I_{\text{dc}}} + \\ \;\;\;\frac{{\partial G}}{{\partial (D{I_{\text{dc}}})}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta (D{I_{\text{dc}}}) + \frac{{\partial G}}{{\partial ({D^2}{I_{\text{dc}}})}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta ({D^2}{I_{\text{dc}}}) + \\ \;\;\;\frac{{\partial G}}{{\partial {P_{\text{loss}}}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {P_{\text{loss}}} + \frac{{\partial G}}{{\partial (D{P_{\text{loss}}})}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta (D{P_{\text{loss}}}) + \\ \;\;\;\frac{{\partial G}}{{\partial ({D^2}{P_{\text{loss}}})}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta ({D^2}{P_{\text{loss}}}) + \frac{{\partial G}}{{\partial {P_\text{t}}}}{|_{\text{(E}\text{.P}\text{.)}}}\varDelta {P_\text{t}} + \text{(H}\text{.O}\text{.T)} = 0 \\ \end{array} $ | (29) |
系统稳态运行点可表示为
| $\begin{array}{l} \text{(E}\text{.P}\text{.)} = ({U_{\text{dc - 0}}}, D{U_{\text{dc - 0}}}, {D^2}{U_{\text{dc - 0}}}, {I_{\text{dc - 0}}}, D{I_{\text{dc - 0}}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;{D^2}{I_{\text{dc - }0}}, {P_{\text{loss - 0}}}, D{P_{\text{loss - 0}}}, {D^2}{P_{\text{loss - 0}}}, {P_{\text{t}{\rm{ - }}0}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;({U_{\text{dc0}}}, 0, 0, {I_{\text{dc0}}}, 0, 0, {P_{\text{loss}0}}, 0, 0, {P_{\text{t0}}}) \\ \end{array} $ | (30) |
将式(30)代入式(29)可得到换流器直流侧线性化小信号动态方程:
| $\begin{array}{l} {I_{\text{dc}0}}\varDelta {U_{\text{dc}}} + ({C_{\text{eq}}}{U_{\text{dc}0}} - {L_{\text{eq}}}(\frac{{P_{\text{loss}0}^2}}{{U_{\text{dc}0}^3}} + \frac{{{I_{\text{dc0}}}{P_{\text{loss}0}}}}{{U_{\text{dc0}}^2}})) \\ \;\;\;\;\varDelta (D{U_{\text{dc}}}) - {C_{\text{eq}}}{L_{\text{eq}}}\frac{{{P_{\text{loss}0}}}}{{{U_{\text{dc}0}}}}\varDelta ({D^2}{U_{\text{dc}}}) + \\ \;\;\;\;\;{U_{\text{dc0}}}\varDelta {I_{\text{dc}}} + ({L_{\text{eq}}}{I_{\text{dc0}}} + {L_{\text{eq}}}\frac{{{P_{\text{loss}0}}}}{{{U_{\text{dc}0}}}})\varDelta (D{I_{\text{dc}}}) + \\ \;\;\;\;{C_{\text{eq}}}{L_{\text{eq}}}{U_{\text{dc}0}}\varDelta ({D^2}{I_{\text{dc}}}) + \varDelta {P_{\text{loss}}} + ({L_{\text{eq}}}\frac{{{P_{\text{loss}0}}}}{{U_{\text{dc}0}^2}} + \\ \;\;\;\;{L_{\text{eq}}}\frac{{{I_{\text{dc}0}}}}{{{U_{\text{dc0}}}}})\varDelta (D{P_{\text{loss}}}) + {C_{\text{eq}}}{L_{\text{eq}}}\varDelta ({D^2}{P_{\text{loss}}}) - \varDelta {P_\text{t}} = 0 \\ \end{array} $ | (31) |
对式(31)进行拉氏变换可得:
| $\begin{array}{l} [ - {C_{\text{eq}}}{L_{\text{eq}}}\frac{{{P_{\text{loss}0}}}}{{{U_{\text{dc}0}}}}{s^2} + ({C_{\text{eq}}}{U_{\text{dc0}}} - {L_{\text{eq}}}(\frac{{P_{\text{loss}0}^2}}{{U_{\text{dc}0}^3}} + \frac{{{I_{\text{dc}0}}{P_{\text{loss}0}}}}{{U_{\text{dc}0}^2}}))s + \\ \;\;{I_{\text{dc}0}}]\varDelta {U_{\text{dc}}} + ({C_{\text{eq}}}{L_{\text{eq}}}{U_{\text{dc}0}}{s^2} + ({L_{\text{eq}}}{I_{\text{dc0}}} + {L_{\text{eq}}}\frac{{{P_{\text{loss0}}}}}{{{U_{\text{dc0}}}}})s + {U_{\text{dc0}}}) \\ \;\;\varDelta {I_{\text{dc}}} + ({C_{\text{eq}}}{L_{\text{eq}}}{s^2} + ({L_{\text{eq}}}\frac{{{P_{\text{loss0}}}}}{{U_{\text{dc0}}^2}} + {L_{\text{eq}}}\frac{{{I_{\text{dc0}}}}}{{{U_{\text{dc}0}}}})s + 1)\varDelta {P_{\text{loss}}} = \varDelta {P_\text{t}} \\ \end{array} $ | (32) |
式(32)即为换流器直流侧有功功率Pdc的小信号动态方程。
1.3.4 全局下垂控制并网VSC模型由式(23)和(32)可以得到换流器交直流侧功率平衡方程为
| $\begin{array}{l} 1.5{I_{d0}}\varDelta {U_{\text{sd}}} + ( - 1.5L{I_{d0}}{\rm{s}} + 1.5{U_{sd0}} - 3R{I_{d0}})\varDelta {I_d} - \\ \;\;\;\;(1.5L{I_{q0}}s + 3R{I_{q0}})\varDelta {I_q} = [ - {C_{\text{eq}}}{L_{\text{eq}}}\frac{{{P_{\text{loss0}}}}}{{{U_{\text{dc0}}}}}{s^2} + \\ \;\;\;\;\;({C_{\text{eq}}}{U_{\text{dc}0}} - {L_{\text{eq}}}(\frac{{P_{\text{loss}0}^2}}{{U_{\text{dc}0}^3}} + \frac{{{I_{\text{dc}0}}{P_{\text{loss}}}}}{{U_{\text{dc}0}^2}}))s + {I_{\text{dc}0}}]\varDelta {U_{\text{dc}}} + \\ \;\;\;\;\;({C_{\text{eq}}}{L_{\text{eq}}}{U_{\text{dc}0}}{s^2} + ({L_{\text{eq}}}{I_{\text{dc}0}} + {L_{\text{eq}}}\frac{{{P_{\text{loss}0}}}}{{{U_{\text{dc}0}}}})s + {U_{\text{dc0}}})\varDelta {I_{\text{dc}}} + \\ \;\;\;\;\;({C_{\text{eq}}}{L_{\text{eq}}}{s^2} + ({L_{\text{eq}}}\frac{{{P_{\text{loss}0}}}}{{U_{\text{dc0}}^\text{2}}} + {L_{\text{eq}}}\frac{{{I_{\text{dc}0}}}}{{{U_{\text{dc0}}}}})s + 1)\varDelta {P_{\text{loss}}} = \varDelta {P_\text{t}} \\ \end{array} $ | (33) |
将其化简为
| $\begin{array}{l} A\varDelta {U_{\text{sd}}} + B\varDelta {I_d} + C\varDelta {I_q} = D\varDelta {U_{\text{dc}}} + E\varDelta {I_{\text{dc}}} + F\varDelta {P_{\text{loss}}} \Rightarrow \\ \;\;\varDelta {U_{\text{dc}}} = \frac{B}{D}\varDelta {I_d} + \frac{A}{D}\varDelta {U_{\text{sd}}} + \frac{C}{D}\varDelta {I_q} - \frac{E}{D}\varDelta {I_{\text{dc}}} - \frac{F}{D}\varDelta {P_{\text{loss}}} \\ \end{array} $ | (34) |
其中:
| $\left\{ \begin{array}{l} A \triangleq 1.5{I_{d0}}\;\;\;\;\; \\ B \triangleq - 1.5{L_s}{I_{d0}}s + 1.5{U_{sd0}} - 3R{I_{{\rm{d}}0}} \\ C \triangleq - 1.5{L_s}{I_{q0}}s - 3R{I_{q0}} \\ \begin{array}{*{20}{c}} \begin{array}{l} D \triangleq [ - {C_{\text{eq}}}{L_{\text{eq}}}\frac{{{P_{\text{loss}0}}}}{{{U_{\text{dc0}}}}}{s^2} + ({C_{\text{eq}}}{U_{\text{dc}0}} - \\ \;\;\;\;\;\;\;{L_{\text{eq}}}(\frac{{P_{\text{loss0}}^\text{2}}}{{U_{\text{dc}0}^3}} + \frac{{{I_{\text{dc0}}}{P_{\text{loss0}}}}}{{U_{\text{dc0}}^\text{2}}}))s + {I_{\text{dc0}}}] \\ \end{array} &{} \end{array} \\ E \triangleq ({C_{\text{eq}}}{L_{\text{eq}}}{U_{\text{dc}0}}{s^2} + ({L_{\text{eq}}}{I_{\text{dc}0}} + {L_{\text{eq}}}\frac{{{P_{\text{loss0}}}}}{{{U_{\text{dc}0}}}})s + {U_{\text{dc}0}}) \\ F \triangleq ({C_{\text{eq}}}{L_{\text{eq}}}{s^2} + ({L_{\text{eq}}}\frac{{{P_{\text{loss0}}}}}{{U_{\text{dc}0}^2}} + {L_{\text{eq}}}\frac{{{I_{\text{dc0}}}}}{{{U_{\text{dc}0}}}})s + 1) \\ \end{array} \right.$ | (35) |
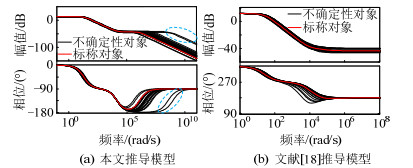
图 5为本文推导ΔId至ΔUdc的传递函数(即控制对象)与文献[18]的对比波德图,由于系统稳态运行点的改变,控制对象可能由最小相位系统(逆变状态)变化到非最小相位系统(整流状态),此时即需要鲁棒控制的参与。从本文推导过程来看,由于考虑了换流器和开关器件的功率损耗、直流侧电感、电容,使得该模型能够更精确地量化系统参数变化时传递函数的响应,将更有利于保证后续鲁棒控制器设计的合理高效。
|
图 5 控制对象波德图比较 Fig. 5 Bode diagram comparison of control objects |
结合全局下垂控制器可得:
| ${T_u}D{U_{\text{ref}}} = {k_e}(U_{\text{dc}}^\text{*} - {U_{\text{bus}}}) - {\rm{d}}{I_{\text{dc}}}$ | (36) |
由于直流母线电压参考值
| $\varDelta {U_{\text{ref}}} = - \frac{{{k_e}}}{{{T_u}s}}\varDelta {U_{\text{bus}}} - \frac{d}{{{T_u}s}}\varDelta {I_{\text{dc}}}$ | (37) |
换流器直流侧出口电压Udc与直流母线电压Ubus关系为(省略了拉普拉斯算子s):
| $\varDelta {U_{\text{dc}}} = \varDelta {U_{\text{bus}}} + {R_l}\varDelta {I_{\text{dc}}} + {L_l}s\varDelta {I_{\text{dc}}}$ | (38) |
因此,由式(37)和(38)可得:
| $\varDelta {U_{\text{ref}}} = - \frac{{{k_e}}}{{{T_u}s}}\varDelta {U_{\text{dc}}} + (\frac{{{k_e}{R_l} - d}}{{{T_u}s}} + \frac{{{k_e}{L_l}}}{{{T_u}}})\varDelta {I_{\text{dc}}}$ | (39) |
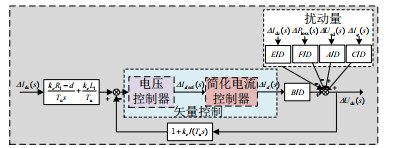
结合式(34)、(35)和(39)可得到全局下垂控制电压源换流器直流母线电压小信号动态特性,如图 6所示。由该控制结构可知,直流母线电压不仅受系统内参数(交直流侧滤波器、下垂系数、稳态工作运行点)摄动的影响,还受ΔUsd和ΔIq等扰动量的影响,这为鲁棒控制器设计提供了明确的研究对象。
|
图 6 全局下垂控制电压源换流器直流母线电压小信号动态结构 Fig. 6 Small-signal DC-link dynamics model of a UDC-based VSC |
对于直流电网而言,由于网架结构的多样性,电压源换流器可能用于连接不同类型的直流/交流源和负荷,而随着这些对频率具有强依赖性的单元不断接入或退出运行,势必会对直流母线电压的稳定性造成影响。因此,研究考虑交直流侧瞬时功率、系统参数不确定性和扰动等因素的直流电压鲁棒控制器具有十分重要的意义。
基于鲁棒控制理论中对系统不确定性的定义,本文对于VSC全局下垂鲁棒控制器设计过程中的不确定性划分为非结构化不确定性和参数化不确定性,前者对应于图 7中的d轴电流控制器,后者主要包括直流侧电容Ceq,直流侧电感Leq,下垂系数d,全局下垂系数ke。
|
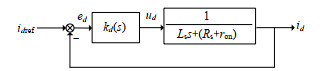
图 7 VSC电流控制简化模型 Fig. 7 Simplified block diagram of current-controlled VSC system |
VSC双环控制中的d轴电流控制环节如图 7所示,其可简化为图 6中的电流控制环节。
图 7中,kd(s)为双环控制中的电流内环:
| ${k_d}(s) = {k_{pi}} + \frac{1}{{{k_{ii}}s}}$ | (40) |
因此,idref到id的开环传递函数为
| $\iota (s) = (\frac{{{k_{pi}}}}{{{L_\text{s}}s}})\frac{{s + 1{\rm{/}}({k_{pi}}{k_{ii}})}}{{s + (R + {r_{\text{on}}}){\rm{/}}{L_\text{s}}}}$ | (41) |
由式(41)可以看出开环极点为s=-(R+ron)/Ls,由于其十分靠近原点,因此从相对较低的频率开始传递函数前向通道的幅值和相位就开始降低,有可能与开环零点s=-1/(kpikii)产生相消的情况,相应开环传递函数变为
| ${G_i}(s) = \frac{{\iota (s)}}{{1 + \iota (s)}} = \frac{{{I_d}(s)}}{{{I_{d{\rm{ref}}}}(s)}} = \frac{1}{{{\tau _i}s + 1}}$ | (42) |
式中
在实际仿真或者实验过程中,Ls和Rs+ron的值往往固定不变,但在控制器参数调试过程中电流内环控制器的参数kpi和kii通常很难同时满足以上两个条件,二者分别求出的τi值有较小的误差范围。此处Gi(s)为一个估计模型,除参数摄动这种可定量描述的不确定性之外,可能还会产生一些不可预测的非线性扰动。因此本文利用乘积不确定性模型对其进行建模,电流控制器Gi(s)标称传递函数为
| ${\bar G_i}(s) = \frac{1}{{{{\bar \tau }_i}s + 1}}$ | (43) |
式中
利用乘积不确定性建模后的扰动传递函数[19]
| ${G_i}(s) = (1 + {W_{{\tau _i}}}{\delta _{{\tau _i}}}){\bar G_i}(s)$ | (44) |
式中
| $\frac{{{\rm{|}}{G_i}({\rm{j}}\omega ) - {{\bar G}_i}({\rm{j}}\omega ){\rm{|}}}}{{{\rm{|}}{{\bar G}_i}({\rm{j}}\omega ){\rm{|}}}} < {\rm{|}}{W_{{\tau _i}}}({\rm{j}}\omega ){\rm{|}}$ | (45) |
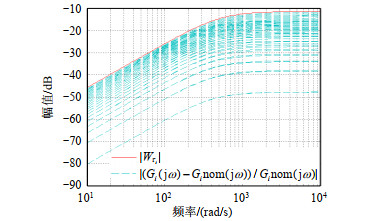
因此,可以通过图 8得到一阶传递函数
|
图 8 电流控制器不确定性近似 Fig. 8 Current controller uncertainty approximations |
在进行系统参数化不确定性建模之前,首先需要明确本文VSC控制系统中涉及的参数化不确定物理量为直流侧电容Ceq、直流侧电感Leq、下垂系统d、全局下垂系数ke 4个参数,其标称值分别为7800μF、0.1mH、0.05、10,摄动范围分别为5000μF≤Ceq≤12000μF、0≤Leq≤2mH、0≤d≤0.2、8≤ke≤20。将图 6的结构转化为状态空间形式,并最终通过MATLAB软件计算得到系统不确定模型[20](因文章篇幅限制,该状态空间模型在此省略)。
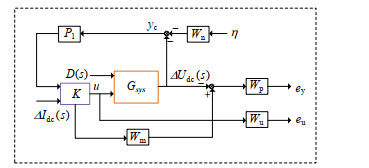
2.3 基于μ-综合鲁棒控制器设计为了达到直流母线电压控制效果和提高系统抗扰能力,本文采用图 9所示的2自由度换流器电压鲁棒控制闭环设计结构。其中Gsys为考虑不确定性的VSC控制系统,K为鲁棒控制器,另外包括1个参考输入ΔIdc(s),1个随机噪声信号η(满足||η2|| < 1),2个输出成本信号ey和eu,u为鲁棒控制器输出信号,yc为反馈信号与噪声的叠加反馈信号,Pl为参考直流电压到参考直流电流传递函数。
| ${P_\text{l}} = (1 + \frac{{{k_e}}}{{{T_u}s}}){\rm{/}}(\frac{{{k_e}{R_\text{l}} - d}}{{{T_u}s}} + \frac{{{k_e}{L_\text{l}}}}{{{T_u}}})$ | (46) |
|
图 9 换流器系统闭环互联结构 Fig. 9 Closed-loop interconnection structure of VSC system |
除此之外,Wm为设计闭环系统与之匹配的理想动态结构,根据本文研究系统的采样频率和控制器带宽选择为
令Δp表示μ-综合设计过程中的不确定性集合:
| ${\varDelta _p} = \left\{ {\left[ {\begin{array}{*{20}{c}} \varDelta &0 \\ 0&{{\varDelta _F}} \end{array}} \right]} \right\}$ | (47) |
式中:Δ表示上文建立的系统参数化不确定性和非结构化不确定性集合; ΔF为一个虚拟不确定性模块; Δp输入为ey、eu,输出为外部外部输入ΔIdc(s)、D(s)、η。控制器K满足系统稳定鲁棒性和性能鲁棒性的要求,需要在每个频率ω∈[0, ∝]处,结构奇异值μ满足条件[19-20]:
| $\mu _{{\varDelta _P}}^{}({F_L}(P, K)({\rm{j}}\omega )) < 1$ | (48) |
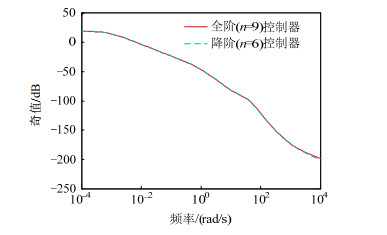
由于本文涉及三端VSC系统,其中VSC2和VSC3参数相同,VSC1输出线路阻抗与前两者不同,因此以VSC2/VSC3为例进行μ-综合D-K迭代计算。式(49)即为9阶鲁棒控制器,降阶得到式(50)所示6阶鲁棒控制器,由图 10可看出控制效果基本一致。
| $\begin{array}{l} {{K'}_{\text{VSC2(VSC}3)}} = \frac{{ - 2.45 \times {{10}^{ - 12}}{s^9} + 1.063 \times {{10}^{ - 6}}{s^8} + 0.04965{s^7} + 131.9{s^6} + 1.295 \times {{10}^5}{s^5} + 5.522 \times {{10}^7}{s^4} + }}{{{s^9} + 4.103 \times {{10}^4}{s^8} + 4.147 \times {{10}^7}{s^7} + 1.231 \times {{10}^{10}}{s^6} + 9.555 \times {{10}^{11}}{s^5} + 3.844 \times {{10}^{13}}{s^4} + }} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{9.559 \times {{10}^9}{s^3} + 4.737 \times {{10}^{11}}{s^2} + 4.834 \times {{10}^{12}}s + 1.366 \times {{10}^6}}}{{7.424 \times {{10}^{14}}{s^3} + 7.072 \times {{10}^{14}}{s^2} + 5.496 \times {{10}^{11}}s + 1.314 \times {{10}^5}}} \\ \end{array} $ | (49) |
| ${K_{\text{VSC2(VSC}3)}} = \frac{{ - 2.45 \times {{10}^{ - 12}}{s^6} + 9.151 \times {{10}^{ - 7}}{s^5} + 0.0023{s^4} + 0.873{s^3} + 51.44{s^2} + 546.8s + 1.545 \times {{10}^{ - 4}}}}{{{s^6} + 91.33{s^5} + 4020{s^4} + 8.366 \times {{10}^4}{s^3} + 8 \times {{10}^4}{s^2} + 62.17s + 1.486 \times {{10}^{ - 5}}}}$ | (50) |
| ${K_{\text{VSC1}}} = \frac{{ - 7.35 \times {{10}^{ - 12}}{s^6} + 1.684 \times {{10}^{ - 6}}{s^5} + 0.003987{s^4} + 1.437{s^3} + 82.66{s^2} + 781.7s + 1.751 \times {{10}^{ - 4}}}}{{{s^6} + 95.52{s^5} + 4420{s^4} + 9.597 \times {{10}^4}{s^3} + 9.211 \times {{10}^4}{s^2} + 48.27s + 1.703 \times {{10}^{ - 5}}}}$ | (51) |
|
图 10 全阶和降阶鲁棒控制器作用时系统结构奇异值 Fig. 10 Structured singular value of uncertain model with full-order and reduced-order robust controller |
对于换流站VSC1,可计算得到降阶鲁棒控制器如式(51)所示,因计算原理相同,过程在此省略。最终,基于上述工作,得到了如图 4所示的基于全局下垂鲁棒控制的直流配电网控制结构。
3 稳定性分析通常在闭环反馈调节下,换流器在控制带宽内的输入端表现为恒功率负载,输入阻抗呈负增量特性[21-22]。虽然每个子系统都被设计为独立的稳定系统,但是由多个电力电子装置控制的子系统组成的直流配网系统可能会由于恒功率负载而引起子系统间的相互作用,大幅改变各单元独立工作情况下的控制器带宽,将对系统稳定性造成不利影响。因此,本节首先对全局下垂鲁棒控制的VSC单元输出阻抗进行建模,分析各控制参数对于VSC输出阻抗的影响,继而对系统中光伏发电并网单元、直流线路和恒阻抗负载进行建模,利用Middlebrook稳定性判据对系统稳定性进行分析[23-25]。
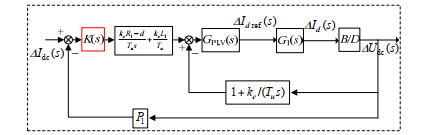
3.1 全局下垂鲁棒控制VSC输出阻抗建模及小信号稳定性分析基于图 6中对于换流器直流侧输出电压的小信号建模及分析,可得到图 11所示的等效模型。其中,K(s)为基于全局下垂鲁棒控制器,GPI, V(s)为传统VSCs双闭环控制中的d轴外环PI控制器,Gi(s)为电流简化模型,B/D见式(35)。由于此处已有鲁棒
|
图 11 换流器输出直流电压控制小信号模型 Fig. 11 Small-signal model of VSC DC-link voltage control |
控制器作用,因此在进行计算时均取系统标称值。
| $\left\{ {\begin{array}{*{20}{l}} {{G_{PI, V}}(s) = {k_{pv}} + \frac{1}{{{k_{iv}}s}}} \\ {{G_i}(s) = \frac{1}{{{\tau _i}s + 1}}} \end{array}} \right.$ | (52) |
图 11中的闭环传递函数Gcl(s)为
| $\begin{array}{l} {G_{\text{cl}}}(s) = \frac{{{G_{\operatorname{PI} , V}}(s){G_i}(s){G_1}(s){G_2}(s)K(s)}}{{1 + {G_{PI, V}}(s){G_i}(s){G_2}(s){G_3}(s) + }} \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{G_{\operatorname{PI} , V}}(s){G_i}(s){G_1}(s){G_2}(s)K(s)}}{{{G_{PI, V}}(s){G_i}(s){G_1}(s){G_2}(s){P_l}(s)K(s)}} \\ \end{array} $ | (53) |
式中
全局下垂鲁棒控制方式下VSC的输出阻抗为
| ${Z_{\text{robust}}}(s) = - {G_{\text{cl}}}(s)$ | (54) |
由于VSC出口线路阻抗会对其输出阻抗造成影响,而本文VSC1和VSC2、VSC3的线路阻抗设置不同,本节中将以VSC2为例对输出阻抗影响因素进行分析。为与全局下垂、传统下垂控制的VSC进行比较,给出全局下垂控制作用时VSC的输出阻抗为
| ${Z_{\text{UDC}}}(s) = - \frac{{{G_{PI, V}}(s){G_i}(s){G_1}(s){G_2}(s)}}{{1 + {G_{PI, V}}(s){G_i}(s){G_2}(s){G_3}(s)}}$ | (55) |
传统下垂控制作用时VSC的输出阻抗为
| ${Z_d}(s) = \frac{{{G_{\operatorname{PI} , V}}(s){G_i}(s){G_2}(s)d}}{{1 + {G_{PI, V}}(s){G_i}(s){G_2}(s)}}$ | (56) |
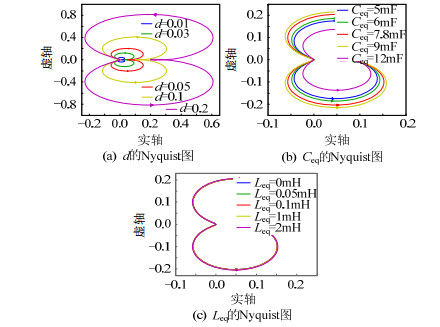
图 12-14为3种控制方式下VSC输出阻抗奈奎斯特曲线。由此可看出,基于全局下垂鲁棒控制、全局下垂控制和传统下垂控制分别作用于VSC闭环控制时,其输出阻抗的奈奎斯特曲线均没有包围(-1, 0)点,即均满足稳定的充要条件。由图 13可看出,全局下垂控制作用时,ke、d、Rl、Ceq变化均会对换流器输出阻抗奈奎斯特曲线造成不同程度的影响,当参数变化范围达到一定范围时,可能会使对应奈奎斯特曲线包围(-1, 0)点,导致系统失稳。而对于全局下垂鲁棒控制而言,虽然其作用时稳定裕度相对较低,但始终保持在稳定域内,参数取不同数值时,奈奎斯特曲线不会发生变化,从换流器输出阻抗的角度验证本文设计的基于全局下垂鲁棒控制对于参数变化的鲁棒控制能力。

|
图 12 系统参数变化时全局下垂鲁棒控制VSC输出阻抗奈奎斯特曲线 Fig. 12 Nyquist diagram of VSC output impedance with UDC-based robust control under system parameters variations |
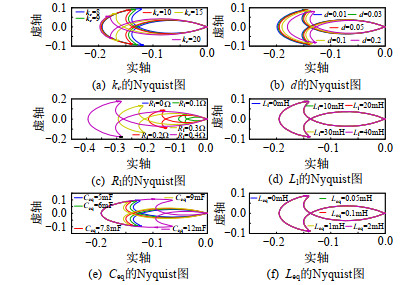
|
图 13 系统参数变化时全局下垂控制VSC输出阻抗奈奎斯特曲线 Fig. 13 Nyquist diagram of VSC output impedance with UDC under system parameters variations |
|
图 14 系统参数变化时传统下垂控制VSC输出阻抗奈奎斯特曲线 Fig. 14 Nyquist diagram of VSC output impedance with traditional droop control under system parameters variations |
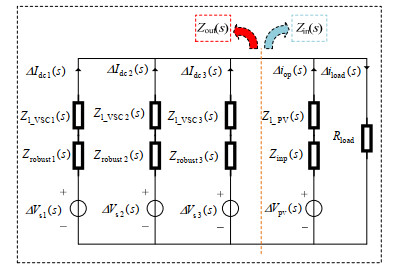
由Middlebrook稳定性判据及直流配网中与公共直流母线相连的各端口输出/输入阻抗建模分析,可得到如图 15所示的基于全局下垂鲁棒控制下的戴维南等效电路。其中,VSC1、VSC2、VSC3用于控制直流母线电压,因此将其作为源单元处理,光伏单元由于工作于MPPT控制模式,将其和恒阻抗负载一起作为荷单元处理。
|
图 15 基于全局下垂鲁棒控制下的戴维南等效电路 Fig. 15 Thevenin equivalent circuit with UDC-based robust control |
图 15中,Zout(s)和Zin(s)分别为系统源输出阻抗和荷输入阻抗。Zrobust1(s)、Zrobust2(s)、Zrobust3(s)分别为全局下垂鲁棒控制下各VSC单元等效输出阻抗,Zinp(s)为PV及其并网单元等效输出阻抗。考虑文章篇幅限制,线路阻抗和光伏并网单元输入阻抗计算过程在此省略,可参考文献[21]。
Zout(s)和Zin(s)分别为
| $\begin{array}{l} {Z_{\text{out}}} = ({Z_{\text{robust1}}} + {Z_{\text{l}\_\text{VSC}1}}){\rm{//}} \\ \;\;\;\;\;\;\;\;\;({Z_{\text{robust2}}} + {Z_{\text{l_VSC}2}}){\rm{//}}({Z_{\text{robust3}}} + {Z_{\text{l_VSC}3}}) \\ \end{array} $ | (57) |
| ${Z_{\text{in}}}(s) = ({Z_{\text{inp}}} + {Z_{\text{l_pv}}}){\rm{//}}{R_{\text{load}}}$ | (58) |
根据Middlebrook稳定性判据,系统次环路增益Ts为
| $\begin{array}{l} {T_\text{s}} = \frac{{{Z_{\text{out}}}}}{{{Z_{\text{in}}}}} = \\ \frac{{({Z_{\text{robust1}}} + {Z_{\text{l_VSC1}}}){\rm{//}}({Z_{\text{robust2}}} + {Z_{\text{l_VSC2}}}){\rm{//}}({Z_{\text{robust3}}} + {Z_{\text{l_VSC3}}})}}{{({Z_{\text{inp}}} + {Z_{\text{l_pv}}}){\rm{//}}{R_{\text{load}}}}} \\ \end{array} $ | (59) |
VSC2和VSC3出口直流线路阻抗取值与VSC1和PV出口直流线路阻抗均不同,为便于分析,将4组参数变化步长及范围取为相同,不会影响分析结果的正确性。
图 16为全局下垂鲁棒控制时系统参数变化次环路增益奈奎斯特曲线,其中图 16(a)-(f)对应物理量与图 12相同。当VSC采用全局下垂鲁棒控制时,图 12已验证其输出阻抗奈奎斯特曲线不易受ke、d、Rl、Ceq和Leq影响,由图 16亦可看出,直流配电系统次环路增益Ts同样不易受以上5个因素影响。从图 16(c)看出,Rl仍会对系统稳定性造成影响,甚至出现失稳,其原因是本文在进行鲁棒控制设计时并没有对Rl进行参数化建模或非结构化扰动建模,因此只要在系统不确定性建模中增加对Rl变化的考虑,就能避免出现图 16(c)的情况,本文不再赘述。

|
图 16 系统参数变化时全局下垂鲁棒控制次环路增益奈奎斯特曲线 Fig. 16 Nyquist diagram of minor loop gain with UDC-based robust control under system parameters variations |
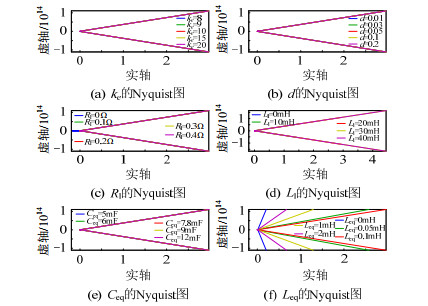
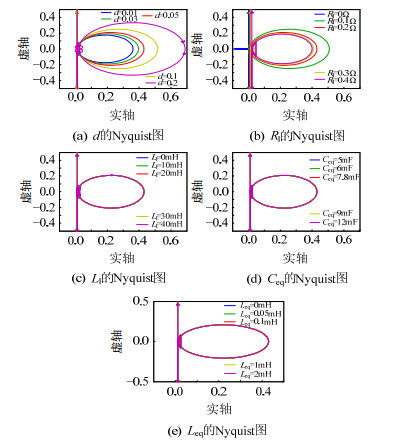
图 17为全局下垂控制时系统参数变化次环路增益奈奎斯特曲线,各图对应物理量同图 13。不同于图 13,全局下垂控制下换流器输出阻抗奈奎斯特曲线不包围(-1, 0)点,换流器系统为稳定状态,而图 17,全局下垂控制时系统次环路增益奈奎斯特曲线虽然不包围(-1, 0)点,但其距原点距离无限增大,即波德图中的幅值无限增大,系统有可能发生失稳。这也验证了互联系统和子系统稳定性之间的关系,即互联系统的子系统均稳定时,并不能保证互联系统也稳定。图 18为系统参数变化时传统下垂控制次环路增益奈奎斯特曲线,与图 16相比,下垂系数d闭环仍然会对系统稳定性造成影响,而Rl则对两种控制方式均会产生影响,就影响程度而言,传统下垂控制较小,但传统下垂控制对于各系统参数变化时直流母线电压的控制能力远不如本文所提出的全局下垂鲁棒控制,具体内容将在第4节介绍。
|
图 17 系统参数变化时全局下垂控制次环路增益奈奎斯特曲线 Fig. 17 Nyquist diagram of minor loop gain with UDC under system parameters variations |
|
图 18 系统参数变化时传统下垂控制次环路增益奈奎斯特曲线 Fig. 18 Nyquist diagram of minor loop gain with traditional droop control under system parameters variations |
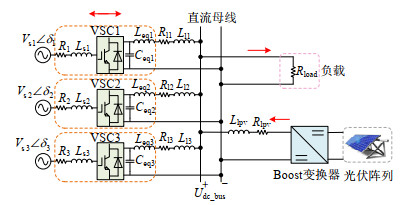
本文利用图 19所示的一个典型三端直流配网,在PSCAD/EMTDC软件中对上述设计的控制器效果进行验证。其主要分为3个区域,控制母线电压稳定的VSC1、VSC2、VSC3分别与380V、50Hz的交流电网连接构成第1区域,通过传统下垂控制/全局下垂控制/基于全局下垂的鲁棒控制对换流器直流侧出口电流进行管理,以准确维持母线电压稳定; 第2区域为通过Boost升压直流变压器与直流配网母线相连的光伏模块; 第3区域为配置无源负载的直流微网。在第1区域中,3种控制方法分别运用于控制器中,以比较其控制效果的差异。第2区域中的Boost换流器采用传统PI控制器,其余详细的系统参数及控制器参数见表 1-3。
|
图 19 仿真测试系统 Fig. 19 The test system in the simulation |
|
|
表 1 仿真系统参数 Table 1 System parameters of the simulation |
|
|
表 2 光伏系统仿真参数 Table 2 Simulation parameters of PV system |
|
|
表 3 仿真控制参数 Table 3 Controller parameters of the simulation |
首先,为验证全局下垂控制器对于换流器直流侧电流等比例控制的有效性,本节将对传统下垂控制和全局下垂控制进行仿真分析,VSC1、VSC2、VSC3于0.2s连接于直流母线,下垂控制系数均为0.05kV/kA,在0.4s时0.28MW的静态阻性负荷连接于直流配网,温度为20℃、辐射强度为600W/m2的光伏模块在3.5s时连接于直流母线,最后5.5s时另一0.14MW的静态阻性负荷接入。
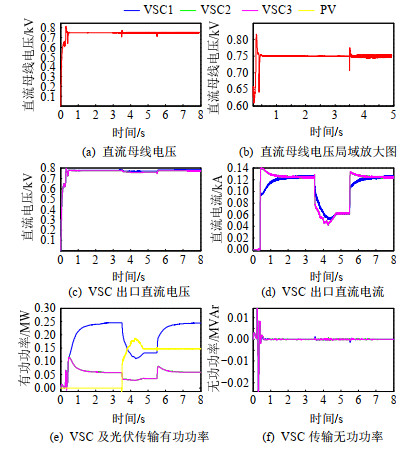
图 20、21分别为上述仿真工况下传统下垂控制、全局下垂控制作用于VSC1、VSC2、VSC3时系统仿真结果。

|
图 20 传统下垂控制系统性能 Fig. 20 Traditional droop control-based system performance |
由图 20(a)显示的母线直流电压运行水平可知,与上文理论分析结果一致,直流母线电压在0.2s至0.4s系统空载时保持与设定值0.75kV相当的水平。但在0.4s后加入了负载,由于线路阻抗及下垂系数的作用,母线电压相较于额定值有一定的稳态误差, 只有在3.5s加入了光伏单元后母线电压水平才达到期望水平,但这对于母线电压控制来说并不是有利的,因为相较图 21(b)中母线电压受分布式能源接入的影响来看,传统下垂控制的抗扰能力明显不足。不仅如此,从图 21(d)、(e)可以看出,虽然各换流器的额定有功功率相同且控制参数一致,但由于直流出口至直流母线的线路阻抗参数不同,导致其出口电流和承担功率均不同(VSC2和VSC3的输出电流和承担功率始终保持一致,曲线重合)。而从图 21(d)可以看出,Idc1和Idc2、Idc3在较短的时间内就能通过控制器中积分环节而趋向一致,并且在分布式能源接入的情况下也能保证较好的控制效果。
|
图 21 全局下垂控制系统性能 Fig. 21 UDC-based system performance |
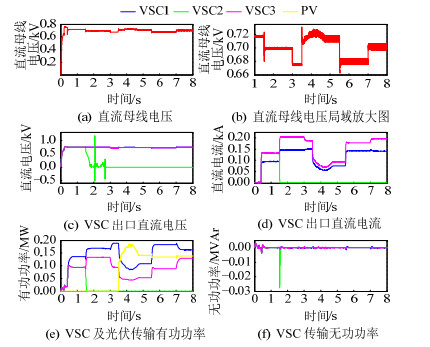
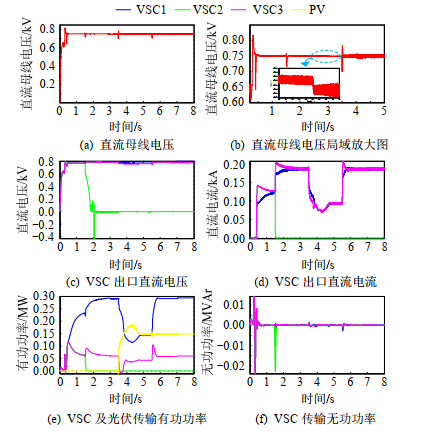
为验证基于全局下垂的鲁棒控制器对于直流母线电压和换流器直流侧电流等比例控制的抗干扰能力和控制的鲁棒性,本节将对传统下垂控制、全局下垂控制和基于全局下垂的鲁棒控制分别进行仿真分析。VSC1、VSC2、VSC3均以0.05kV/kA下垂控制系数于0.2s连接于直流母线,功率0.28MW的静态阻性负荷0.4s时接入母线,1.5s时VSC2因故障退出运行,接着3s时VSC1和VSC3下垂系数由0.05kV/kA变为0.2kV/kA,ke由10变为20(传统下垂控制不涉及ke),温度为20℃,辐射强度为600W/m2的光伏模块于3.5s连接于直流母线,然后在5.5s时另一0.14MW的静态阻性负荷接入母线,最后在7s时VSC1和VSC3下垂系数从0.2kV/kA调整为0.05kV/kA,ke调整为10。仿真结果见图 22-24,各图对应曲线含义与图 20相同。
|
图 22 下垂系数变化和换流器退出运行时传统下垂控制系统性能 Fig. 22 Traditional droop control-based system performance under droop ratio variations and converter outage |
|
图 23 下垂系数变化和换流器退出运行时全局下垂控制系统性能 Fig. 23 UDC-based system performance under droop ratio variations and converter outage |
|
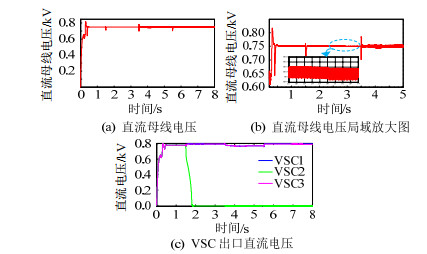
图 24 系统参数变化和换流器退出运行时基于全局下垂鲁棒控制系统性能 Fig. 24 UDC-based robust control system performance under system parameters variations and converter outage |
由图 22(b)和图 23(b)中可看出,在下垂系数变化和换流站退出运行时,传统下垂控制对于直流母线电压的控制能力受到较大影响,实际母线电压在参考值750V上下有较大的波动,始终不能恢复至设定值,特别在3s下垂系数变化和5.5s负荷增加时,电压跌落至675V左右,下降比例近10%,严重影响了母线电压稳定。而全局下垂控制器则对于系统参数变化和换流站退出运行等工况具有更高的抗干扰能力,但在3s和7s还是会受到控制参数变化的轻微影响,从电压波动范围来看较传统下垂控制优化至2%左右。当VSC2在1.5s退出运行时,直流母线电压保持稳定,但两种控制方法下VSC2直流侧端口电压在趋于0的过程中均会不断振荡,甚至出现负压的情况,不满足系统内稳定性。对于换流站直流侧出口电流等比例控制的要求,从图 23(d)中可以看出,在各种干扰作用的情况下,采用所设计全局下垂控制器的各换流站仍能在较短时间内使其各直流侧出口电流趋向一致,不受线路阻抗参数不同的影响。
由图 24可看出,0.4s VSC投入运行后,母线电压在0.06s内恢复稳定,并且直流电压最高至817V左右。1.5s VSC2退出运行后,其直流侧电压无振荡和过零现象。相较图 23中全局下垂控制在3s时受控制参数的轻微影响,加入鲁棒控制后的系统不仅保持了全局下垂控制的性能,同时对于系统参数变化具有更强的抗干扰能力,几乎可忽略所考虑的参数变化对控制效果的影响。在参数摄动范围准确预估的情况下,鲁棒控制器能够最大程度消除其影响,精度控制直流母线电压,保证系统鲁棒性。
5 结论本文在考虑多端直流配网VSC交直流侧瞬时功率的基础上,提出了一种用于直流母线电压控制的全局下垂鲁棒控制器。文中首先建立了全局下垂控制下换流器直流侧出口电压的小信号模型,该模型考虑了全局下垂控制动态响应、交流侧滤波器和直流侧滤波器的瞬时功率以及等效直流电网相关不确定性的影响。为了保证控制器在非结构化不确定性、参数不确定性和随机扰动下的鲁棒稳定性和鲁棒性能,设计了一种基于μ-综合的2自由度鲁棒电压控制器。该控制器结构简单,阶数固定,不需要进行任何调整。此外,控制器还具有良好的性能,可以消除多端直流电网中常见的各种系统不确定性和干扰,如全局下垂系数和下垂斜率变化、换流器退出运行、直流电网和负载参数的变化等,有利于增强多端直流电网的稳定性和鲁棒性。理论分析和仿真结果验证了该控制器的有效性。
| [1] |
熊雄, 季宇, 李蕊, 等. 直流配用电系统关键技术及应用示范综述[J]. 中国电机工程学报, 2018, 38(23): 6802-6813. XIONG Xiong, JI Yu, LI Rui, et al. An overview of key technology and demonstration application of DC distribution and consumption system[J]. Proceedings of the CSEE, 2018, 38(23): 6802-6813 (in Chinese). (  0) 0) |
| [2] |
盛万兴, 李蕊, 李跃, 等. 直流配电电压等级序列与典型网络架构初探[J]. 中国电机工程学报, 2016, 36(13): 3391-3403. SHENG Wanxing, LI Rui, LI Yue, et al. A preliminary study on voltage level sequence and typical network architecture of direct current distribution network[J]. Proceedings of the CSEE, 2016, 36(13): 3391-3403 (in Chinese). (  0) 0) |
| [3] |
刘飞, 熊晓琪, 查鹏程, 等. 直流配电网网架结构与分布式光伏多目标协同优化[J]. 中国电机工程学报, 2020, (12): 3754-3765. LIU Fei, XIONG Xiaoqi, et al. Multi-objective collaborative optimization for DC distribution network configuration and distributed photovoltaic[J]. Proceedings of the CSEE, 2020, (12): 3754-3765(in Chinese). http://www.pcsee.org/CN/abstract/abstract32260.shtml (  0) 0) |
| [4] |
KRISHAN R, VERMA A, MISHRA S. Loadability analysis of DC distribution systems[J]. International Journal of Electrical Power & Energy Systems, 2018, 103: 176-184. (  0) 0) |
| [5] |
GAVRILUTA C, CANDELA J I, ROCABERT J, et al. Adaptive droop for control of multiterminal DC bus integrating energy storage[J]. IEEE Transactions on Power Delivery, 2015, 30(1): 16-24. DOI:10.1109/TPWRD.2014.2352396 (  0) 0) |
| [6] |
桑博, 张涛, 刘亚杰, 等. 多微电网能量管理系统研究综述[J]. 中国电机工程学报, 2020, 40(10): 3077-3093. SANG Bo, ZHANG Tao, et al. Energy management system research of multi-microgrid: a review[J]. Proceedings of the CSEE, 2020, 40(10): 3077-3093(in Chinese). http://www.pcsee.org/CN/abstract/abstract32189.shtml (  0) 0) |
| [7] |
彭乔, 刘天琪, 张英敏, 等. 考虑功率裕度与系统稳定性的直流电网自适应下垂控制[J]. 中国电机工程学报, 2018, 38(12): 3498-3506. PENG Qiao, LIU Tianqi, ZHANG Yingmin, et al. Adaptive droop control of VSC based DC grid considering power margin and system stability[J]. Proceedings of the CSEE, 2018, 38(12): 3498-3506 (in Chinese). (  0) 0) |
| [8] |
LI Xianlin, GUO Li, HONG Chao, et al. Hierarchical control of multiterminal DC grids for large-scale renewable energy integration[J]. IEEE Transactions on Sustainable Energy, 2018, 9(3): 1448-1457. DOI:10.1109/TSTE.2018.2789465 (  0) 0) |
| [9] |
CHEN Xia, ZHOU Jianyu, SHI Mengxuan, et al. A novel virtual resistor and capacitor droop control for HESS in medium-voltage DC system[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2518-2527. DOI:10.1109/TPWRS.2019.2894754 (  0) 0) |
| [10] |
LI Yong, HE Li, LIU Fang, et al. Flexible voltage control strategy considering distributed energy storages for DC distribution network[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 163-172. DOI:10.1109/TSG.2017.2734166 (  0) 0) |
| [11] |
VRANA T K, BEERTEN J, BELMANS R, et al. A classification of DC node voltage control methods for HVDC grids[J]. Electric Power Systems Research, 2013, 103: 137-144. DOI:10.1016/j.epsr.2013.05.001 (  0) 0) |
| [12] |
季一润, 袁志昌, 赵剑锋, 等. 一种适用于柔性直流配电网的电压控制策略[J]. 中国电机工程学报, 2016, 36(2): 335-341. JI Yirun, YUAN Zhichang, ZHAO Jianfeng, et al. A suitable voltage control strategy for DC distribution power network[J]. Proceedings of the CSEE, 2016, 36(2): 335-341 (in Chinese). (  0) 0) |
| [13] |
ZHONG Qingchang. Robust droop controller for accurate proportional load sharing among inverters operated in parallel[J]. IEEE Transactions on Industrial Electronics, 2013, 60(4): 1281-1290. DOI:10.1109/TIE.2011.2146221 (  0) 0) |
| [14] |
ZHONG Qingchang, ZENG Yu. Universal droop control of inverters with different types of output impedance[J]. IEEE Access, 2016, 4: 702-712. DOI:10.1109/ACCESS.2016.2526616 (  0) 0) |
| [15] |
SHUAI Zhikang, HE Dong, FANG Junbin, et al. Robust droop control of DC distribution networks[J]. IET Renewable Power Generation, 2016, 10(6): 807-814. DOI:10.1049/iet-rpg.2015.0455 (  0) 0) |
| [16] |
DAVARI M, MOHAMED Y A R I. Robust Multi-objective control of VSC-based DC-voltage power port in hybrid AC/DC multi-terminal micro-grids[J]. IEEE Transactions on Smart Grid, 2013, 4(3): 1597-1612. DOI:10.1109/TSG.2013.2249541 (  0) 0) |
| [17] |
DAVARI M, MOHAMED Y A R I. Robust droop and DC-bus voltage control for effective stabilization and power sharing in VSC Multiterminal DC grids[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4373-4395. DOI:10.1109/TPEL.2017.2715039 (  0) 0) |
| [18] |
DAVARI M, MOHAMED Y A R I. Dynamics and robust control of a grid-connected VSC in multiterminal DC grids considering the instantaneous power of DC- and AC-Side filters and DC grid uncertainty[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 1942-1958. DOI:10.1109/TPEL.2015.2439645 (  0) 0) |
| [19] |
DOYLE J, FRANCIS B, TANNENBAUM A. Feedback control theory[M]. New York, NY, USA: Macmillan Publishing Co, 1990: 21-160.
(  0) 0) |
| [20] |
GU Dawei, PETKOV P H, KONSTANTINOV M M. Robust control design with MATLAB[M]. 2nd ed. New York, NY, USA: Springer, 2013: 12-584.
(  0) 0) |
| [21] |
张学, 裴玮, 邓卫, 等. 含恒功率负载的交直流混联配电系统稳定性分析[J]. 中国电机工程学报, 2017, 37(19): 5572-5582. ZHANG Xue, PEI Wei, DENG Wei, et al. Stability analysis of AC/DC hybrid distribution system with constant power loads[J]. Proceedings of the CSEE, 2017, 37(19): 5572-5582 (in Chinese). (  0) 0) |
| [22] |
伍文华, 周乐明, 陈燕东, 等. 海上MVDC供电系统的正阻尼重构稳定控制策略[J]. 中国电机工程学报, 2019, 39(3): 696-710+949. WU Wenhua, ZHOU Leming, et al. Stability control strategy with positive-damper reconstructed for the maritime MVDC power supply system[J]. Proceedings of the CSEE, 2019, 39(3): 696-710+949(in Chinese). http://www.pcsee.org/CN/abstract/abstract31120.shtml (  0) 0) |
| [23] |
MIDDLEBROOK R D. Input filter considerations in design and application of switching regulators[C]// Proceedings of the IEEE Conference Record of Annual Meeting of the Industry and General Application Group. Chicago, USA: IEEE, 1976: 366-382.
(  0) 0) |
| [24] |
FENG Xiaogang, LIU Jinjun, LEE F C. Impedance specifications for stable DC distributed power systems[J]. IEEE Transactions on Power Electronics, 2002, 17(2): 157-162. DOI:10.1109/63.988825 (  0) 0) |
| [25] |
LU Xiaonan, SUN Kai, GUERRERO J M, et al. Stability enhancement based on virtual impedance for DC microgrids with constant power loads[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2770-2783. DOI:10.1109/TSG.2015.2455017 (  0) 0) |



 林莉(1974),女,博士,副教授,硕士生导师,研究方向为电力系统运行与控制,
林莉(1974),女,博士,副教授,硕士生导师,研究方向为电力系统运行与控制,